Choosing collision shapes

A collision shape describes the shape and size of a collision object such as a rigid body.

The 19 shape classes

The examples so far have all used spheres, cubes, and/or cylinders. However, those are but 3 of the 19 concrete subclasses of CollisionShape.

The subclasses are summarized here, in lexicographic order, with illustrations and lists of key properties (explained below):

1. Box2dShape

→ convex
→ positive margin
→ precise
→ fully scalable
→ symmetric

box2d

2. BoxCollisionShape

→ convex
→ positive margin
→ precise
→ fully scalable
→ symmetric

box

3. CapsuleCollisionShape

→ convex
→ zero margin
→ precise
→ uniform scaling only
→ symmetric

capsule

4. CompoundCollisionShape

→ neither concave nor convex
→ positive margin
→ precise if-and-only-if all its children are precise
→ scalable to the extent that all its children are scalable

compound

5. ConeCollisionShape

→ convex
→ positive margin
→ imprecise
→ uniform scaling only
→ symmetric

cone

6. ConicalFrustum

→ convex
→ positive margin
→ imprecise
→ limited scalability
→ symmetric

frustum

7. Convex2dShape

→ convex
→ positive margin
→ imprecise
→ scalable to the extent that its base shape is scalable

convex2d

8. CylinderCollisionShape

→ convex
→ positive margin
→ imprecise
→ limited scalability
→ symmetric

cylinder

9. EmptyShape

→ concave
→ positive margin
→ precise
→ fully scalable, but why bother?
→ symmetric

(no image)

10. GImpactCollisionShape

→ concave
→ positive margin
→ precise
→ fully scalable

gimpact

11. HeightfieldCollisionShape

→ concave
→ positive margin
→ precise
→ fully scalable

heightfield

12. HullCollisionShape

→ convex
→ positive margin
→ imprecise
→ fully scalable

hull

13. MeshCollisionShape

→ concave
→ positive margin
→ precise
→ fully scalable

mesh

14. MinkowskiSum

→ convex
→ margin determined by base shapes
→ not scalable

minkowski

15. MultiSphere

→ convex
→ positive margin
→ precise
→ fully scalable

multiSphere

16. PlaneCollisionShape

→ concave and infinite
→ positive margin
→ precise
→ fully scalable, but why bother?

plane

17. SimplexCollisionShape

→ convex
→ positive margin
→ imprecise
→ not scalable

simplex

18. SphereCollisionShape

→ convex
→ zero margin
→ precise
→ uniform scaling only
→ symmetric

sphere

19. SphericalSegment

→ convex
→ positive margin
→ imprecise
→ uniform scaling only
→ symmetric

segment

The CompoundCollisionShape class is especially important because it enables any number of child shapes to be combined into a single compound shape.

Due to limitations of Bullet, collisions between HeightfieldCollisionShape, MeshCollisionShape, and PlaneCollisionShape objects are never detected. However, such objects will collide with objects having compound or convex shapes.

Similarly, collisions between GImpactCollisionShape and PlaneCollisionShape objects are never detected.

Custom shape classes

Furthermore, you can define new shape classes by extending the abstract CustomConvexShape class:

CustomConvexShape

→ convex
→ positive margin
→ imprecise
→ each subclass determines its scalability

CustomConvex

Examples of this are found in the com.github.stephengold.shapes.custom package.

Convex versus concave

The convex collision-shape classes are those that guarantee the convex property: for any 2 locations inside a shape, the line segment connecting those locations lies entirely inside the shape.

Here are 2 equivalent ways to test whether a shape belongs to a convex class:

boolean convexClass = (shape instanceof ConvexShape);
boolean isConvex = shape.isConvex();
assert convexClass == isConvex;
In this context, "convex" is a property of classes, not instances. While specific instances of non-convex classes have the convex property, those classes don’t guarantee it for all instances.

Concave is essentially the opposite of convex, except that compound shapes are regarded as neither convex nor concave. No shape is both convex and concave. To test whether a shape belongs to a concave class, use shape.isConcave().

Margin

All collision-shape subtypes except CapsuleCollisionShape and SphereCollisionShape incorporate a margin, a narrow zone near the surface of the shape. (The word margin refers to both the zone and its thickness.) According to the Bullet User Manual, the purpose of margin is "to improve performance and reliability of the collision detection."

For shapes with positive margin, the default thickness is 0.04 physics-space units.

While methods are provided to alter margins (and the default margin), doing so is not recommended.

Precise versus imprecise

A precise shape is a collision shape whose effective shape (observed in collisions, contact tests, ray tests, and sweep tests) is unaffected by margin. In effect, the margin of a precise shape is internal, so it doesn’t impact the effective shape.

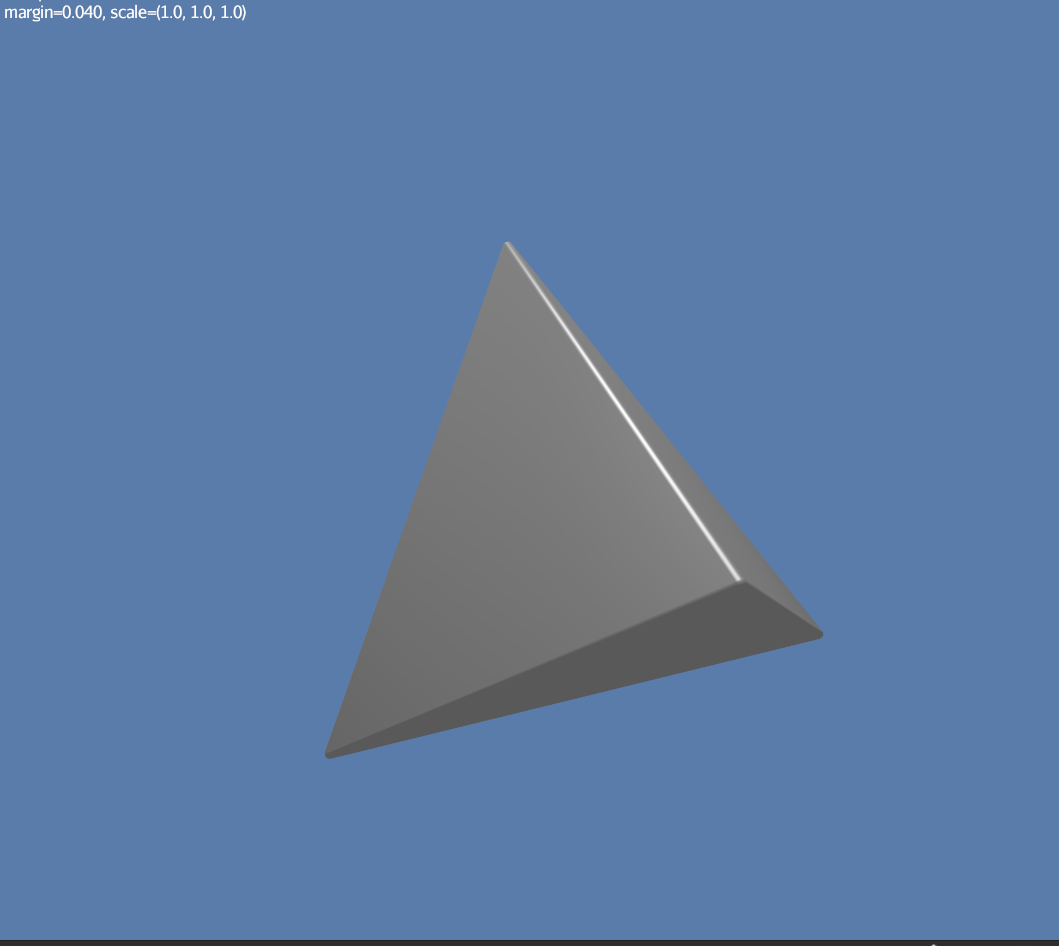
While most collision-shape subtypes are precise, 7 of them are not. For 6 of them, margin uniformly expands their effective shapes:

  1. ConeCollisionShape

  2. ConicalFrustum

  3. Convex2dShape

  4. HullCollisionShape

  5. SimplexCollisionShape

  6. SphericalSegment

To illustrate this, here are 4 otherwise identical simplex shapes with different margins:

margin1

margin4

margin5

margin6

Margin can also distort a CylinderCollisionShape, but its effect there is more complicated: no effect for small margins and non-uniform distortion for large margins.

Since margin is defined in physics-space units, its effects are most noticeable for small shapes.

When using imprecise shapes, you may compensate for margin by shrinking the shape’s dimensions (for a cone shape) or by moving its defining vertices inward (for a simplex or hull shape).

Another possible workaround would be to scale the physics space so as to make the effects of margin less obvious.

Suitability for dynamic bodies

Not all collision shapes are suitable for dynamic rigid bodies.

For instance, collision detection is unreliable between zero-thickness shapes such as:

Furthermore, the following shape classes are suitable only for kinematic or static objects because the simulator cannot determine their mass distributions:

The safest shapes for dynamic rigid bodies are the 7 primitives listed below. All have at least one axis of symmetry, and their centers and axes are well-known:

  1. BoxCollisionShape,

  2. CapsuleCollisionShape,

  3. ConeCollisionShape,

  4. ConicalFrustum,

  5. CylinderCollisionShape,

  6. SphereCollisionShape, and

  7. SphericalSegment.

Many asymmetric shapes are also suitable for dynamic rigid bodies. With such shapes, however, care should be taken to ensure the plausibility of the center of mass and principal axes. At the very least, the shape’s center should be located well inside its convex hull.

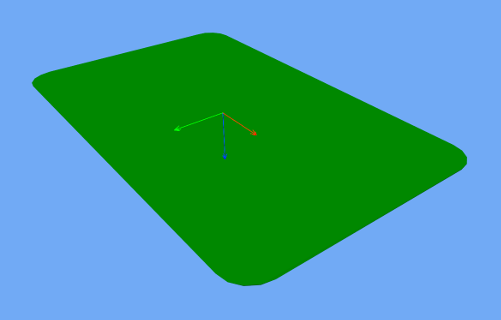
HelloMadMallet (also in Kotlin) is a SPORT app that demonstrates the effect of an implausibly centered shape. Things to notice while running the app:

  1. A dynamic rigid body, shaped like a mallet, falls under the influence of gravity.

  2. Unlike a real mallet, the body’s center of mass (visualized by 3 arrows) is located at the end of its handle.

  3. After landing, the mallet tends to stand erect. Although this orientation seems unnatural, it is the precisely the one that minimizes the mallet’s gravitational potential.

The following classes can be used to generate asymmetric shapes for rigid bodies:

In the case of a CompoundCollisionShape, the principalAxes() and correctAxes() methods may be used to adjust its center and axes for a specific mass distribution.

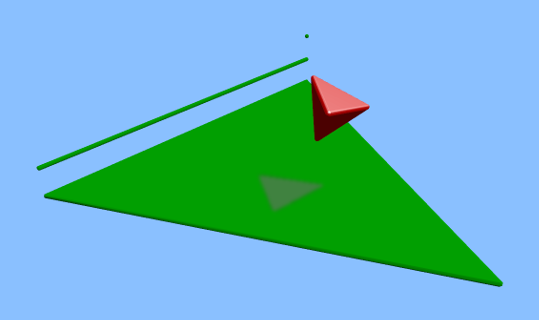
HelloMassDistribution (also in Kotlin) is a SPORT app that demonstrates the use of principalAxes() and correctAxes(). Things to notice while running the app:

  1. This time, the mallet’s center of mass (visualized by 3 arrows) lies much closer to the head, in a very plausible location.

  2. After landing, the mallet comes to rest on its side, which is a natural orientation for a mallet.

The principalAxes() method relies on each child having an accurate center, axes, and moment of inertia.

Scaling

Some applications require collision shapes that are scalable (can be dynamically shrunk or enlarged). However, not all collision shapes can scale arbitrarily. In particular:

You can test at runtime whether a particular scaling is applicable to particular shape:

if (shape.canScale(newScale)) {
    shape.setScale(newScale);
}

Choosing a shape

For efficient simulation, the general rule is: "Use the simplest shape that yields the desired behavior." Focusing on behavior (rather than appearance) helps you avoid simulating details that don’t matter. For instance:

  • A character’s hair should probably be omitted from their collision shape.

  • Any small object that only encounters large, flat surfaces can probably be approximated by a convex hull.

  • As long as a container remains sealed, its collision shape need not be hollow.

Because most 3-D models are composed of triangle meshes, beginners are often tempted to use mesh-based shapes (such as GImpactCollisionShape) for everything. However, since mesh-based collision detection is CPU-intensive, simpler shapes are often a better choice, even when they don’t closely match the model’s shape. In particular, capsule shapes are often used for humanoid models.

The following pseudo-code algorithm may be helpful:

if (the object doesn't move and isn't involved in collisions) {
    use an EmptyShape or don't add the object to the space
} else if (the object doesn't move
           and its shape can be approximated by an infinite plane) {
    use a PlaneCollisionShape
} else if (the object doesn't move
          and its shape can be approximated by point, line segment, or triangle) {
    use a SimplexCollisionShape
} else if (the object doesn't move
           and its shape can be approximated by rectangle) {
    use a Box2dShape
} else if (the object doesn't move
           and its shape can be approximated by 2-D convex polygon) {
    use a Convex2dShape
} else if (its shape can be approximated by a tetrahedron) {
    use a SimplexCollisionShape
} else if (its shape can be approximated by a centered sphere) {
    use a SphereCollisionShape
} else if (its shape can be approximated by a centered rectangular solid) {
    use a BoxCollisionShape
} else if (its shape can be approximated by a centered capsule) {
    use a CapsuleCollisionShape
} else if (its shape can be approximated by a centered cylinder) {
    use a CylinderCollisionShape
} else if (its shape can be approximated by a centered cone) {
    use a ConeCollisionShape
} else if (its shape can be approximated by an ellipsoid
           or an eccentric sphere
           or an eccentric capsule
           or the convex hull of multiple spheres) {
    use a MultiSphere
} else if (its shape can be approximated by an eccentric primitive
           or a combination of convex primitives) {
    use a CompoundCollisionShape
} else if (the object does not move) {
    if (it is a heightfield) {
        use a HeightfieldCollisionShape
    } else {
        use a MeshCollisionShape
    }
} else { // if the object moves
    if (its shape can be approximated by a convex hull) {
        use a HullCollisionShape
    } else if (its shape can be decomposed into convex hulls) {
        use a compound of hull shapes
    } else {
        use a GImpactCollisionShape
    }
}

(Pseudocode adapted from the flowchart on page 13 of the Bullet User Manual.)

GImpactCollisionShape should be your last resort!

Faced with the task of simulating a non-convex rigid body (such as a cross or ring), it’s best to decompose it into convex shapes that, when recombined, will approximate the desired behavior.

There are various approaches, depending how much the developer knows about the object’s shape. If the model’s mesh is generated procedurally, it may be possible to decompose it during the generation process. Or if the object is modeled in Blender, it may be practical to manually decompose it there into meshes that are convex or nearly so.

Automated decomposition

For situations where manual decomposition is impractical, Libbulletjme incorporates Khaled Mamou’s Volumetric-Hierarchical Approximate Convex Decomposition (V-HACD) algorithm. V-HACD makes it easy to decompose a 3-D model into a compound of hull shapes:

// using VHACD version 4:
Vhacd4Parameters v4Parms = new Vhacd4Parameters();
List<Vhacd4Hull> vhacd4Hulls = Vhacd4.compute(meshPositions, meshIndices, v4Parms);
CompoundCollisionShape compound = new CompoundCollisionShape();
for (Vhacd4Hull vhacdHull : vhacd4Hulls) {
    HullCollisionShape hullShape = new HullCollisionShape(vhacdHull);
    compound.addChildShape(hullShape);
}

// or alternatively, using classic VHACD:
VHACDParameters parms = new VHACDParameters();
List<VHACDHull> vhacdHulls = VHACD.compute(meshPositions, meshIndices, parms);
CompoundCollisionShape compound2 = new CompoundCollisionShape();
for (VHACDHull vhacdHull : vhacdHulls) {
    HullCollisionShape hullShape = new HullCollisionShape(vhacdHull);
    compound2.addChildShape(hullShape);
}

The V-HACD algorithm is costly to run, but for many applications it can be run in advance and the output stored until needed. During simulation, the resulting shape will usually be much more efficient than a GImpact shape.

Summary

  • Libbulletjme provides 19 types of collision shapes, ranging from the trivial EmptyShape to the costly GImpactCollisionShape.

  • Collision-shape instances classified as "concave" may still exhibit the convex property.

  • Most collision shapes incorporate a margin.

  • Margin distorts the effective shape of imprecise collision shapes.

  • Most collision shapes can be scaled, but not all can be scaled non-uniformly.

  • Not all collision shapes are suitable for dynamic rigid bodies.

  • Before applying an asymmetric shape to a dynamic rigid body, make sure its center and principal axes are plausible.

  • Use the simplest shape that yields the desired behavior.

  • To speed up simulation of objects with non-convex shapes, decompose them into convex ones, either during model construction or using V-HACD.